Hall, Horowitz, and Jing (1995) "HHJ" Algorithm to Select the Optimal Block-Length
Source:R/hhj.R
hhj.RdPerform the Hall, Horowitz, and Jing (1995) "HHJ" cross-validation algorithm to select the optimal block-length for a bootstrap on dependent data (block-bootstrap). Dependent data such as stationary time series are suitable for usage with the HHJ algorithm.
hhj(
series,
nb = 100L,
n_iter = 10L,
pilot_block_length = NULL,
sub_sample = NULL,
k = "two-sided",
bofb = 1L,
search_grid = NULL,
grid_step = c(1L, 1L),
cl = NULL,
verbose = TRUE,
plots = TRUE
)Arguments
- series
a numeric vector or time series giving the original data for which to find the optimal block-length for.
- nb
an integer value, number of bootstrapped series to compute.
- n_iter
an integer value, maximum number of iterations for the HHJ algorithm to compute.
- pilot_block_length
a numeric value, the block-length (\(l*\) in HHJ) for which to perform initial block bootstraps.
- sub_sample
a numeric value, the length of each overlapping subsample, \(m\) in HHJ.
- k
a character string, either
"bias/variance","one-sided", or"two-sided"depending on the desired object of estimation. If the desired bootstrap statistic is bias or variance then select"bias/variance"which sets \(k = 3\) per HHJ. If the object of estimation is the one-sided or two-sided distribution function, then setk = "one-sided"ork = "two-sided"which sets \(k = 4\) and \(k = 5\), respectively. For the purpose of generating symmetric confidence intervals around an unknown parameter,k = "two-sided"(the default) should be used.- bofb
a numeric value, length of the basic blocks in the block-of-blocks bootstrap, see
m =fortsbootstrapand Kunsch (1989).- search_grid
a numeric value, the range of solutions around \(l*\) to evaluate within the \(MSE\) function after the first iteration. The first iteration will search through all the possible block-lengths unless specified in
grid_step =.- grid_step
a numeric value or vector of at most length 2, the number of steps to increment over the subsample block-lengths when evaluating the \(MSE\) function. If
grid_step = 1then each block-length will be evaluated in the \(MSE\) function. Ifgrid_step > 1, the \(MSE\) function will search over the sequence of block-lengths from1tombygrid_step. Ifgrid_stepis a vector of length 2, the first iteration will step by the first element ofgrid_stepand subsequent iterations will step by the second element.- cl
a cluster object, created by package parallel, doParallel, or snow. If
NULL, no parallelization will be used.- verbose
a logical value, if set to
FALSEthen no interim messages are output to the console. Error messages will still be output. Default isTRUE.- plots
a logical value, if set to
FALSEthen no interim plots are output to the console. Default isTRUE.
Value
an object of class 'hhj'
Details
The HHJ algorithm is computationally intensive as it relies on a cross-validation process using a type of subsampling to estimate the mean squared error (\(MSE\)) incurred by the bootstrap at various block-lengths.
Under-the-hood, hhj() makes use of tsbootstrap,
see Trapletti and Hornik (2020), to perform the moving block-bootstrap
(or the block-of-blocks bootstrap by setting bofb > 1) according
to Kunsch (1989).
References
Adrian Trapletti and Kurt Hornik (2020). tseries: Time Series Analysis and Computational Finance. R package version 0.10-48.
Kunsch, H. (1989) The Jackknife and the Bootstrap for General Stationary Observations. The Annals of Statistics, 17(3), 1217-1241. Retrieved February 16, 2021, from http://www.jstor.org/stable/2241719
Peter Hall, Joel L. Horowitz, Bing-Yi Jing, On blocking rules for the bootstrap with dependent data, Biometrika, Volume 82, Issue 3, September 1995, Pages 561-574, DOI: doi: 10.1093/biomet/82.3.561
Examples
# \donttest{
# Generate AR(1) time series
sim <- stats::arima.sim(list(order = c(1, 0, 0), ar = 0.5),
n = 500, innov = rnorm(500))
# Calculate optimal block length for series
hhj(sim, sub_sample = 10)
#> Pilot block length is: 3
#> Registered S3 method overwritten by 'quantmod':
#> method from
#> as.zoo.data.frame zoo
#> Performing minimization may take some time
#> Calculating MSE for each level in subsample: 10 function evaluations required.
#> Chosen block length: 2 After iteration: 1
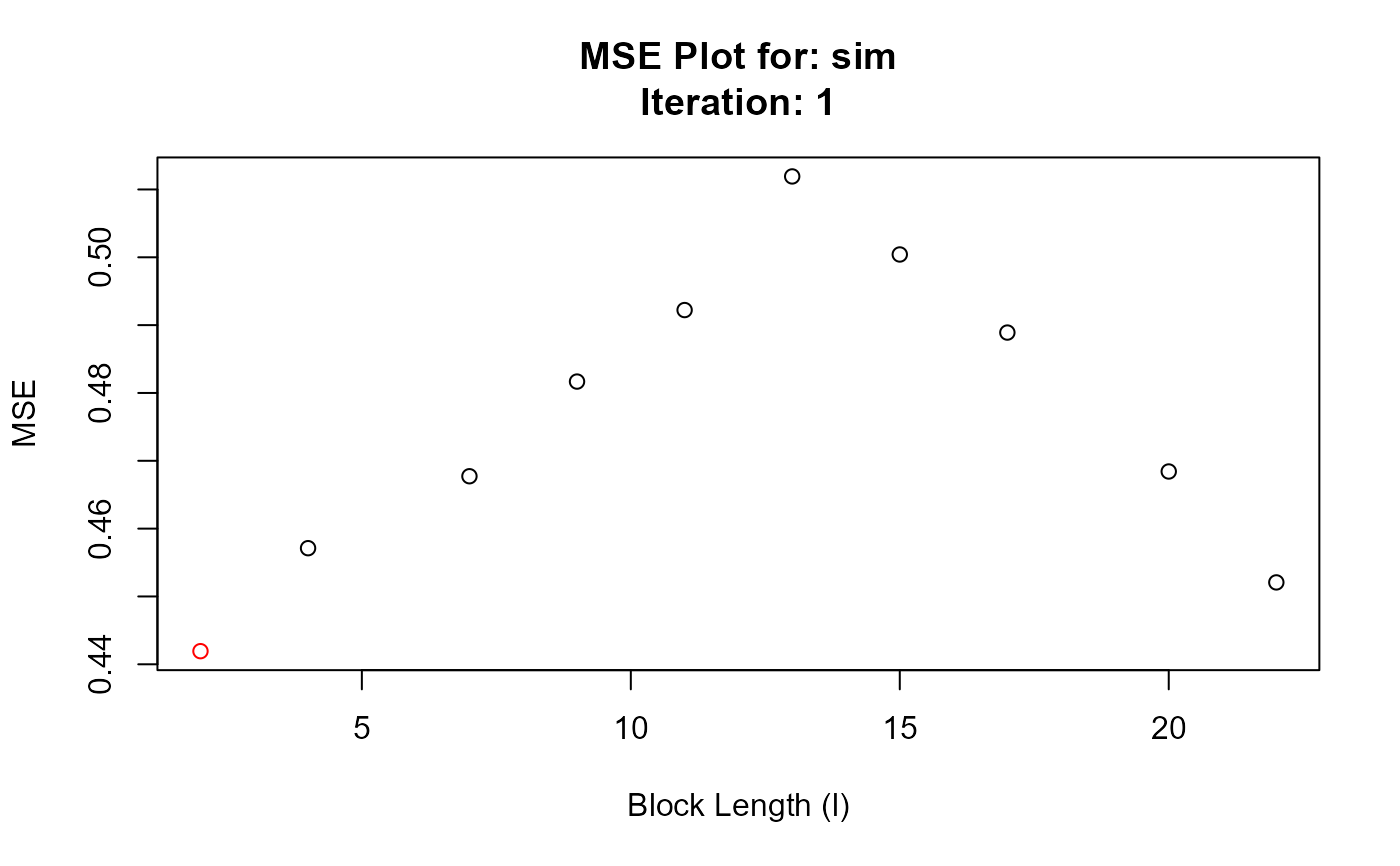 #> Converged at block length (l): 2
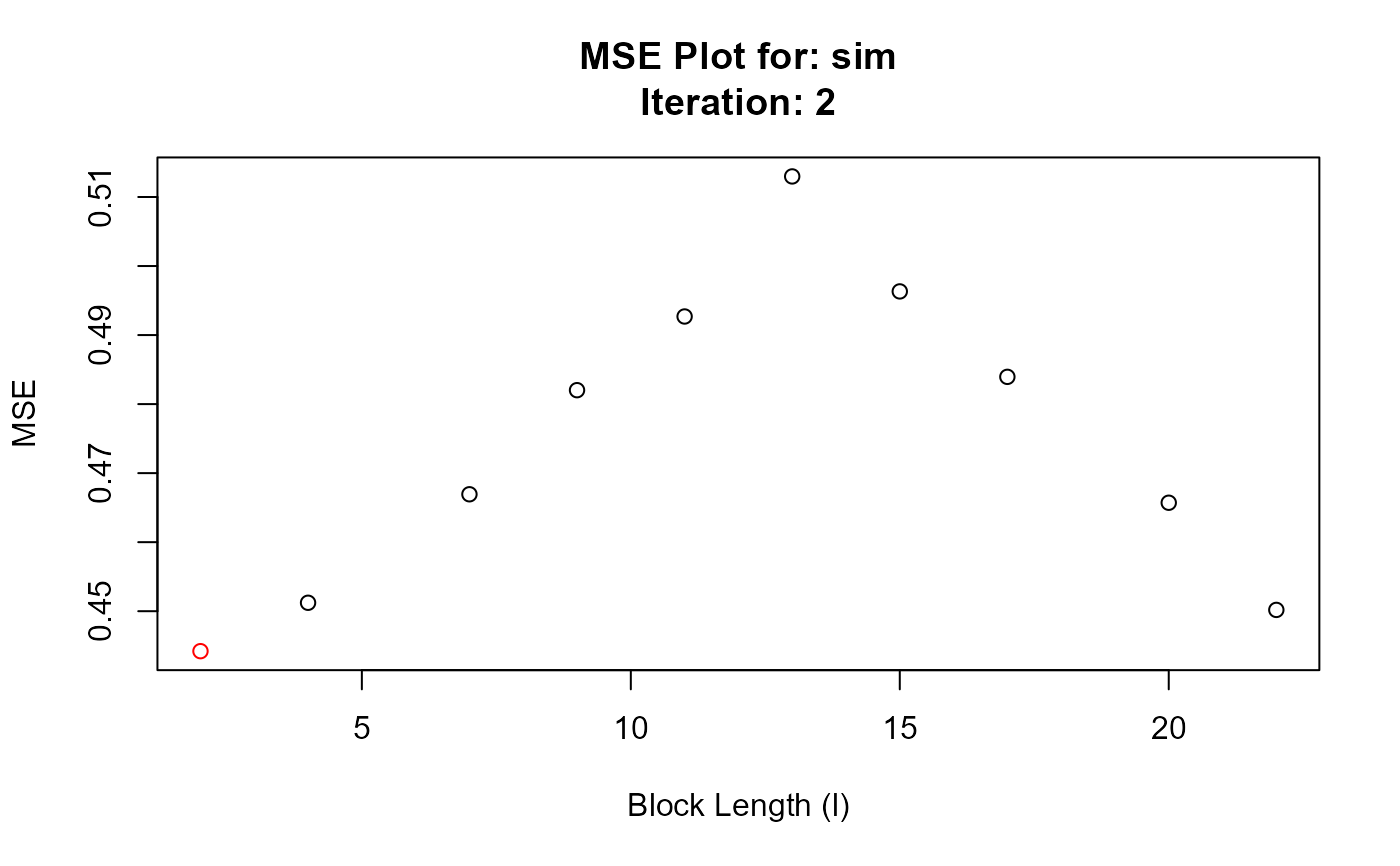
#> Converged at block length (l): 2
 #> $`Optimal Block Length`
#> [1] 2
#>
#> $`Subsample block size (m)`
#> [1] 10
#>
#> $`MSE Data`
#> Iteration BlockLength MSE
#> 1 1 2 0.4419340
#> 2 1 4 0.4571164
#> 3 1 7 0.4677218
#> 4 1 9 0.4816793
#> 5 1 11 0.4922210
#> 6 1 13 0.5119211
#> 7 1 15 0.5004146
#> 8 1 17 0.4889042
#> 9 1 20 0.4684226
#> 10 1 22 0.4520709
#> 11 2 2 0.4442100
#> 12 2 4 0.4512219
#> 13 2 7 0.4669368
#> 14 2 9 0.4820165
#> 15 2 11 0.4926912
#> 16 2 13 0.5129799
#> 17 2 15 0.4963242
#> 18 2 17 0.4839480
#> 19 2 20 0.4657116
#> 20 2 22 0.4501868
#>
#> $Iterations
#> [1] 2
#>
#> $Series
#> [1] "sim"
#>
#> $Call
#> hhj(series = sim, sub_sample = 10)
#>
#> attr(,"class")
#> [1] "hhj"
# Use parallel computing
library(parallel)
# Make cluster object with 2 cores
cl <- makeCluster(2)
# Calculate optimal block length for series
hhj(sim, cl = cl)
#> Pilot block length is: 3
#> Performing minimization may take some time
#> Calculating MSE for each level in subsample: 12 function evaluations required.
#> Chosen block length: 2 After iteration: 1
#> $`Optimal Block Length`
#> [1] 2
#>
#> $`Subsample block size (m)`
#> [1] 10
#>
#> $`MSE Data`
#> Iteration BlockLength MSE
#> 1 1 2 0.4419340
#> 2 1 4 0.4571164
#> 3 1 7 0.4677218
#> 4 1 9 0.4816793
#> 5 1 11 0.4922210
#> 6 1 13 0.5119211
#> 7 1 15 0.5004146
#> 8 1 17 0.4889042
#> 9 1 20 0.4684226
#> 10 1 22 0.4520709
#> 11 2 2 0.4442100
#> 12 2 4 0.4512219
#> 13 2 7 0.4669368
#> 14 2 9 0.4820165
#> 15 2 11 0.4926912
#> 16 2 13 0.5129799
#> 17 2 15 0.4963242
#> 18 2 17 0.4839480
#> 19 2 20 0.4657116
#> 20 2 22 0.4501868
#>
#> $Iterations
#> [1] 2
#>
#> $Series
#> [1] "sim"
#>
#> $Call
#> hhj(series = sim, sub_sample = 10)
#>
#> attr(,"class")
#> [1] "hhj"
# Use parallel computing
library(parallel)
# Make cluster object with 2 cores
cl <- makeCluster(2)
# Calculate optimal block length for series
hhj(sim, cl = cl)
#> Pilot block length is: 3
#> Performing minimization may take some time
#> Calculating MSE for each level in subsample: 12 function evaluations required.
#> Chosen block length: 2 After iteration: 1
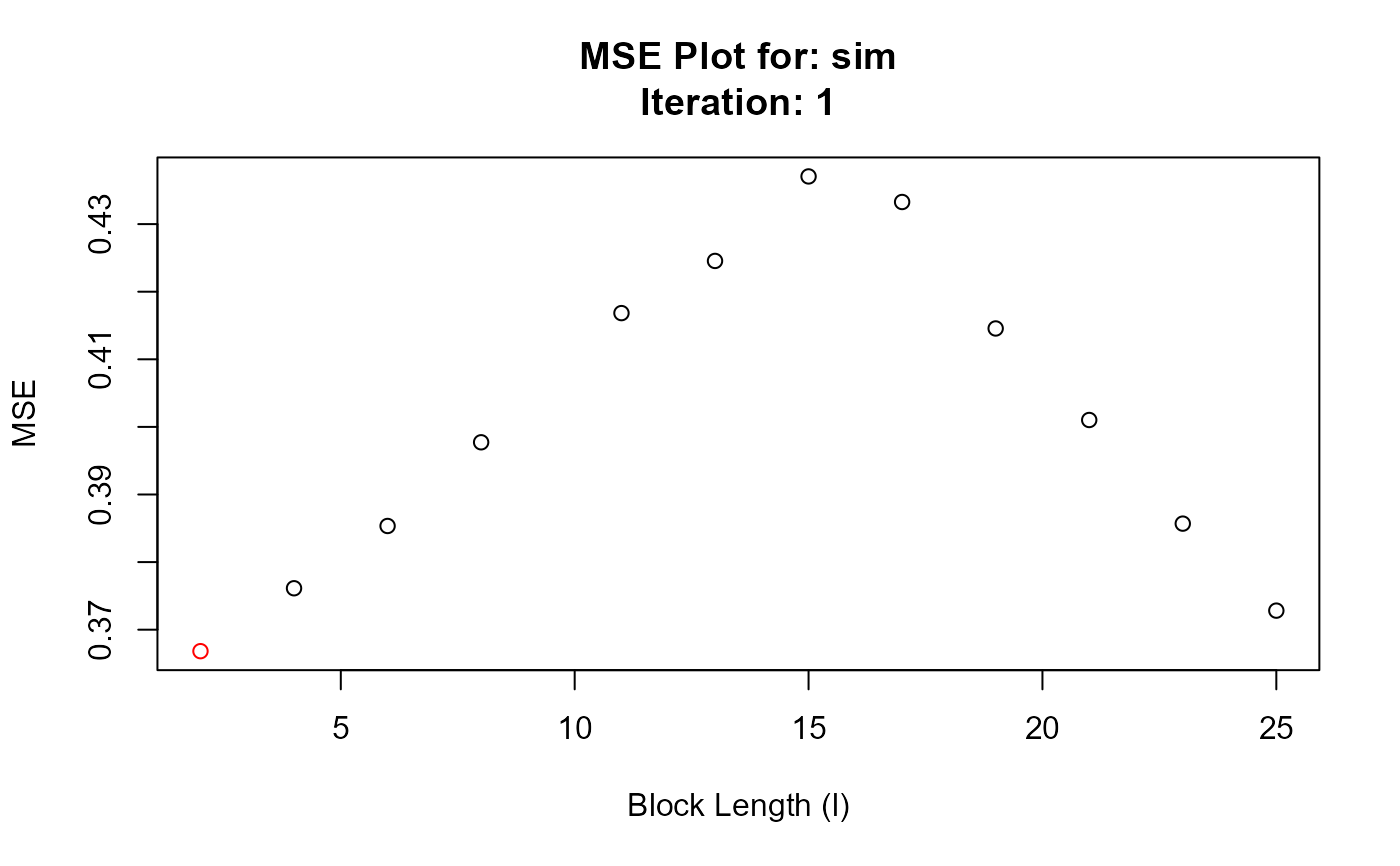 #> Converged at block length (l): 2
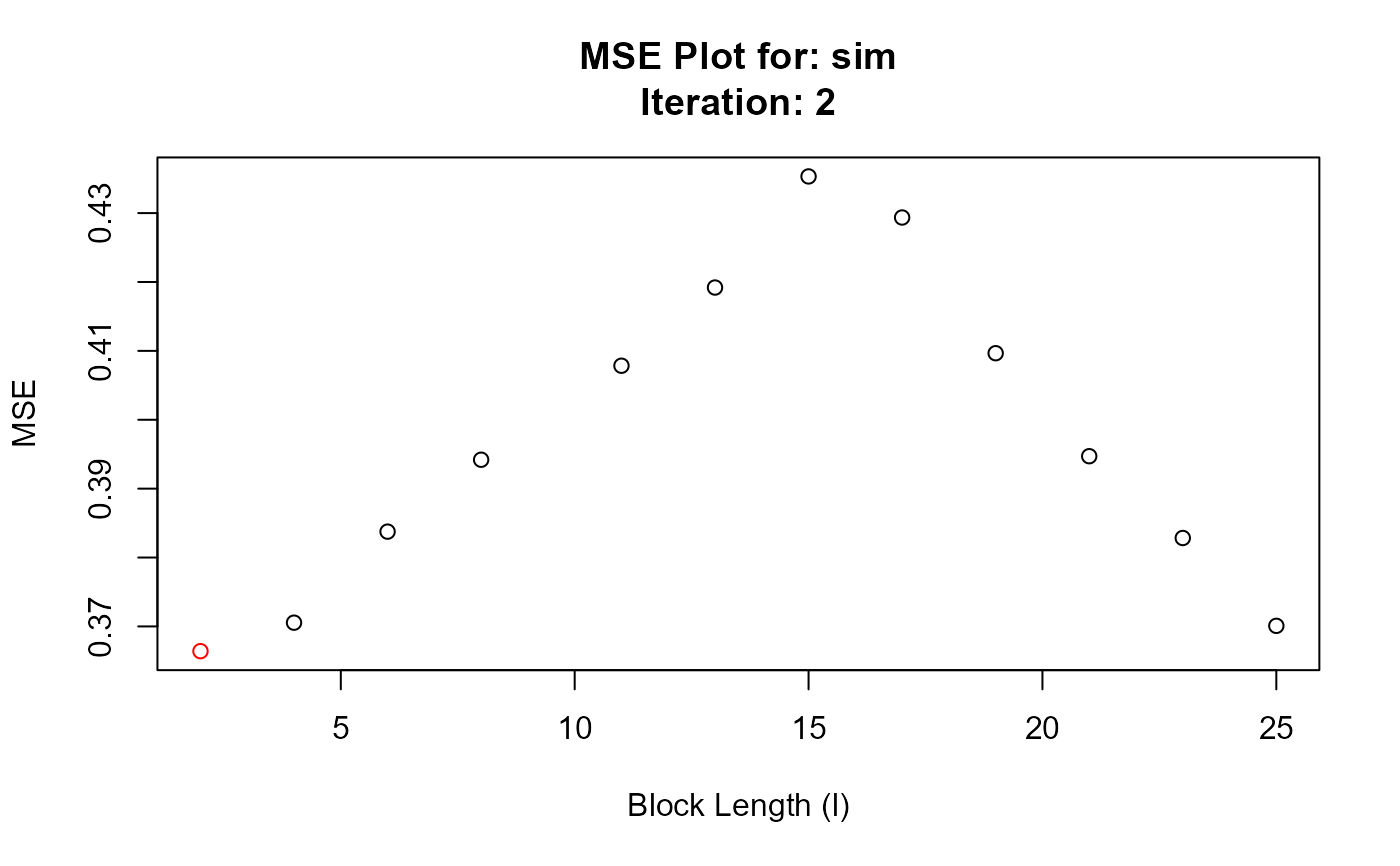
#> Converged at block length (l): 2
 #> $`Optimal Block Length`
#> [1] 2
#>
#> $`Subsample block size (m)`
#> [1] 12
#>
#> $`MSE Data`
#> Iteration BlockLength MSE
#> 1 1 2 0.3668226
#> 2 1 4 0.3761291
#> 3 1 6 0.3853421
#> 4 1 8 0.3977224
#> 5 1 11 0.4168339
#> 6 1 13 0.4245521
#> 7 1 15 0.4370531
#> 8 1 17 0.4332702
#> 9 1 19 0.4145613
#> 10 1 21 0.4010213
#> 11 1 23 0.3856908
#> 12 1 25 0.3728201
#> 13 2 2 0.3664069
#> 14 2 4 0.3705433
#> 15 2 6 0.3837595
#> 16 2 8 0.3941971
#> 17 2 11 0.4078439
#> 18 2 13 0.4191938
#> 19 2 15 0.4353235
#> 20 2 17 0.4293602
#> 21 2 19 0.4096597
#> 22 2 21 0.3947089
#> 23 2 23 0.3828346
#> 24 2 25 0.3700843
#>
#> $Iterations
#> [1] 2
#>
#> $Series
#> [1] "sim"
#>
#> $Call
#> hhj(series = sim, cl = cl)
#>
#> attr(,"class")
#> [1] "hhj"
# }
#> $`Optimal Block Length`
#> [1] 2
#>
#> $`Subsample block size (m)`
#> [1] 12
#>
#> $`MSE Data`
#> Iteration BlockLength MSE
#> 1 1 2 0.3668226
#> 2 1 4 0.3761291
#> 3 1 6 0.3853421
#> 4 1 8 0.3977224
#> 5 1 11 0.4168339
#> 6 1 13 0.4245521
#> 7 1 15 0.4370531
#> 8 1 17 0.4332702
#> 9 1 19 0.4145613
#> 10 1 21 0.4010213
#> 11 1 23 0.3856908
#> 12 1 25 0.3728201
#> 13 2 2 0.3664069
#> 14 2 4 0.3705433
#> 15 2 6 0.3837595
#> 16 2 8 0.3941971
#> 17 2 11 0.4078439
#> 18 2 13 0.4191938
#> 19 2 15 0.4353235
#> 20 2 17 0.4293602
#> 21 2 19 0.4096597
#> 22 2 21 0.3947089
#> 23 2 23 0.3828346
#> 24 2 25 0.3700843
#>
#> $Iterations
#> [1] 2
#>
#> $Series
#> [1] "sim"
#>
#> $Call
#> hhj(series = sim, cl = cl)
#>
#> attr(,"class")
#> [1] "hhj"
# }